Crypto Redacted RSA 1

I have a RSA private key, but it is partially redacted. Can you recover that? Run openssl pkeyutl -decrypt -inkey key-recovered.pem -in encrypted.txt -out plaintext.txt after you have recovered the key.

First, you turn the Pem to Hex using cyberchef.

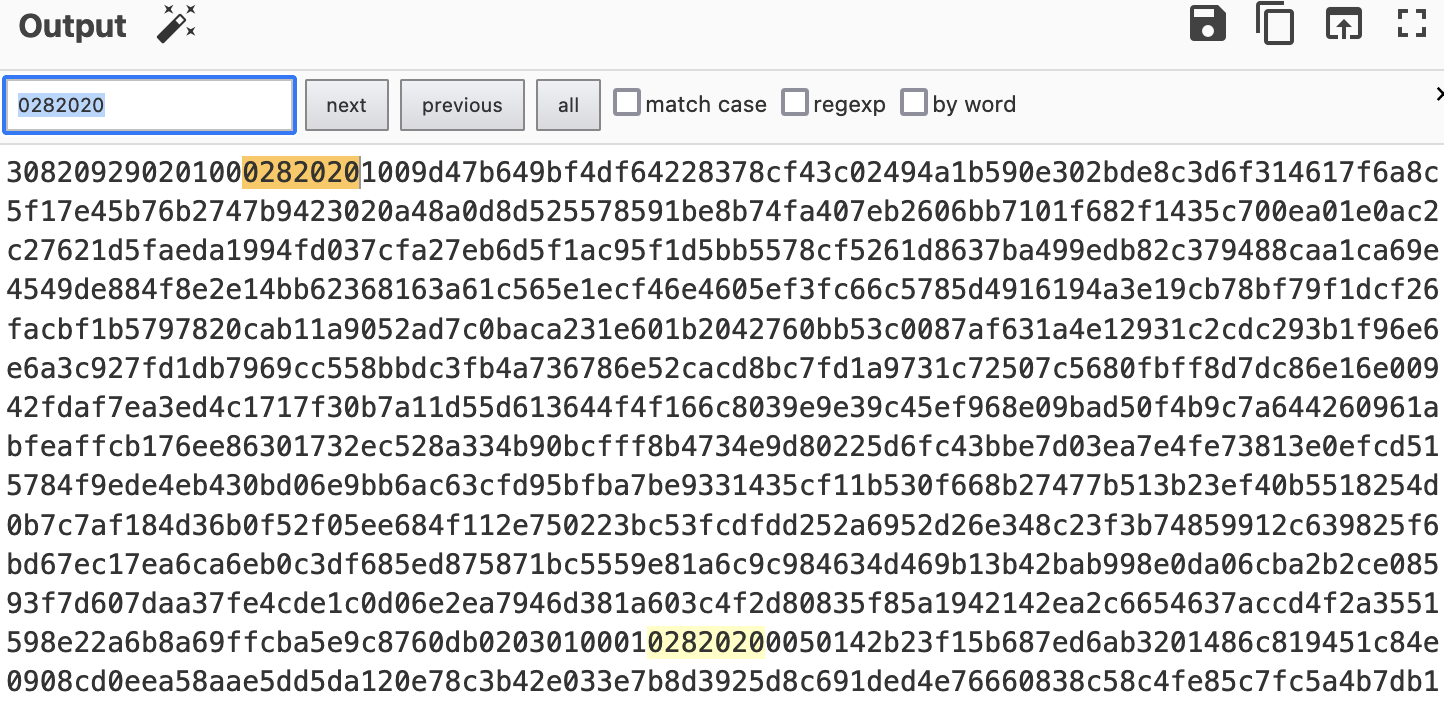
Basically, only the bottom part of it was redacted. So we only need to understand the whole structure:

Structure of PEM in DER

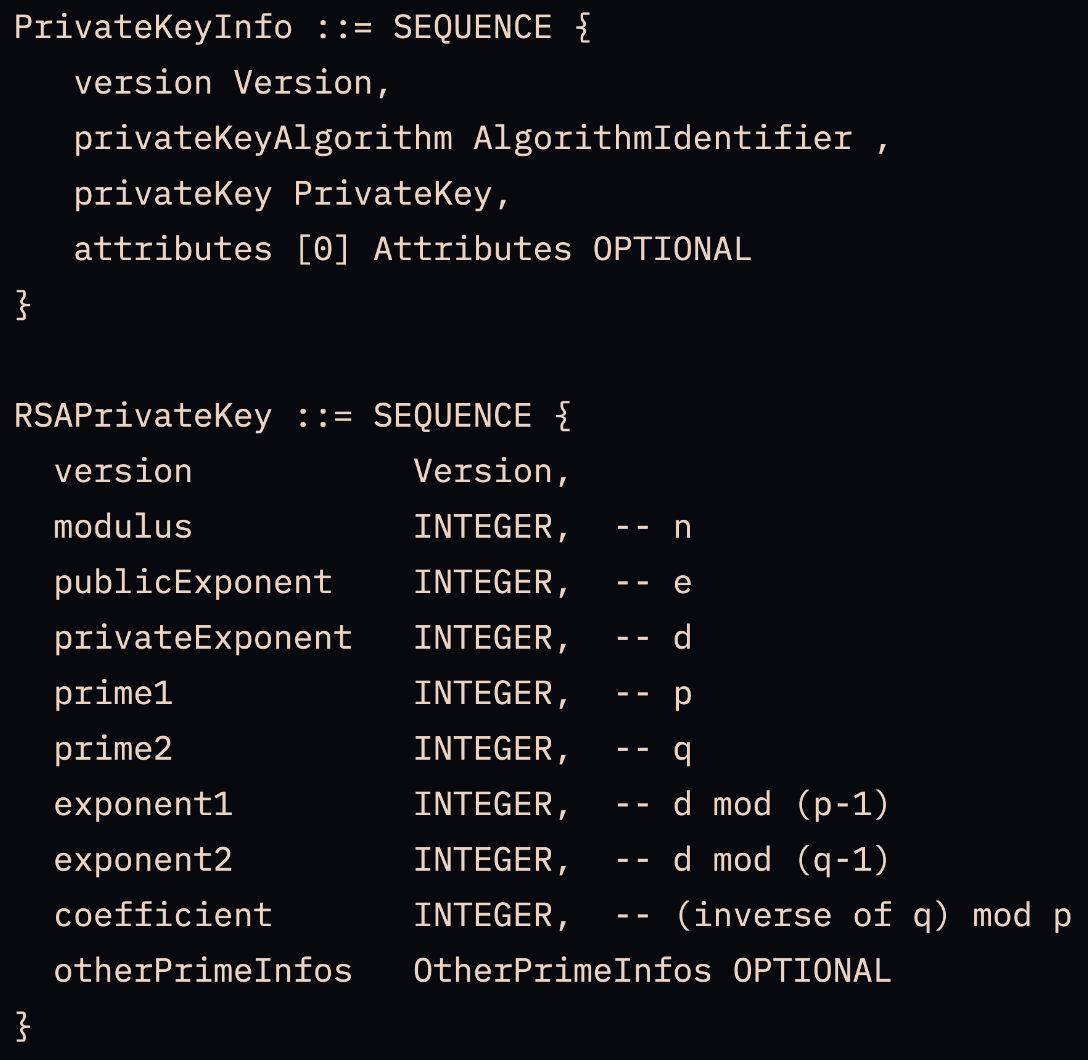
ASN.1 Cheatsheets

Format: (type) (byte size @ length in bytes)

[!NOTE] 1 byte = 2 Hex

Type:

02: INTEGER
04: OCTET STRING (a sequence of bytes)
06: OBJECT IDENTIFIER (like a unique name)
05: NULL (no value)
30: SEQUENCE (a collection of items)

Byte Size @ length:

82: the next 2 bytes are the length
03: 3 bytes
01: 1 byte

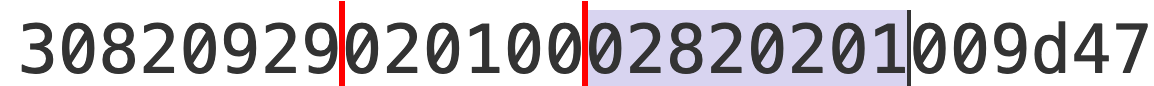
The first column means:

30: structure type (the whole PEM)
82: next 2 bytes are the length
0929: length in hex value

The second column means:

02: integer type
01: next 1 byte is the length
00: length 0

Starting from the third column onwards, shows the N, e, d, p, q ,... and so on

02: integer type
82: next 2 bytes are the length
0201: decimal 513 bytes (1026 hexa digits)
009d47... after 0201 (513 bytes) is the N modular

After I extracted the data, I found the complete of n, e, d:

text

n = {LARGE_HEX}
e = 01001 (65537 normal value)
d = {LARGE_HEX}

after this just run this code to generate a pem file

python

from Crypto.PublicKey import RSA

# Replace these with your values
n = int("YOUR_N_VALUE", 16)  # Replace with the hexadecimal value of n
e = int("YOUR_E_VALUE", 16)  # Usually e is 65537
d = int("YOUR_D_VALUE", 16)  # Replace with the hexadecimal value of d

# Construct the key
key = RSA.construct((n, e, d))

# Export the private key in PEM format
with open("key-recovered.pem", "wb") as f:
    f.write(key.export_key())

alternative without pem file (by neno)

python

Nstr="" # N in string
dstr="" # d in string
encrypted_hex="" # the encrypted.txt in hex

import base64
from Crypto.PublicKey import RSA
from Crypto.Util import number

ciphertext = base64.b64decode(encrypted_hex)
N = int(Nstr, 16)
d = int(dstr, 16)

ciphertext_int = number.bytes_to_long(ciphertext)

# Perform RSA decryption: M = C^d % N
decrypted_int = pow(ciphertext_int, d, N)

# Step 4: Convert the decrypted integer back to a string
decrypted_message = number.long_to_bytes(decrypted_int).decode('latin-1')

print("Decrypted Message:", decrypted_message)

Crypto Redacted RSA 2

This one is same as RSA 1 but the redaction covered up the middle and the bottom (only parts of it showed).

Same strategy, read the Pem in Hex with cyberchef and extract the data:

Here's some useful data extracted:

text

n = {LARGE_NUMBER}
e = {010001} #65537
dp = d mod (q-1) = {LARGE_NUMBER}

So, for a valid PEM, I need to get p or q or d.

How can we find it without large computing power?

Welp, time to google! I found this stackexchange forum particularly helpful for this.

So, chatgpt it, and here's the code:

python

import random
from math import gcd
from sympy import mod_inverse  # To compute modular inverse

def hex_to_int(hex_value):
    """
    Convert a hex string to an integer.
    """
    return int(hex_value, 16)

def find_dp(n, e, dp):
    """
    Find the factorization of n and recover d using dp.
    """
    # Choose a random r
    r = random.randint(2, n - 1)

    # Compute r^(e * dp) mod n
    r_exp = pow(r, e * dp, n)

    # Compute gcd of n and (r_exp - r)
    factor = gcd(n, r_exp - r)

    if factor == 1 or factor == n:
        print("Failed to find a factor. Try again.")
        return None

    # Factorization of n: p and q
    p = factor
    q = n // p

    # Recover private key components
    phi = (p - 1) * (q - 1)
    d = mod_inverse(e, phi)

    return d, p, q

# Example inputs (hexadecimal values)
n_hex = "8D23"  # Replace with your modulus in hex
e_hex = "11"    # Replace with your public exponent in hex
dp_hex = "0D"   # Replace with your dp (d mod (p-1)) in hex

# Convert hex to integers
n = hex_to_int(n_hex)
e = hex_to_int(e_hex)
dp = hex_to_int(dp_hex)

# Find d and factors
result = find_dp(n, e, dp)
if result:
    d, p, q = result
    print(f"Recovered d: {hex(d)}")  # Convert to hex for readability
    print(f"Factors p: {hex(p)}, q: {hex(q)}")  # Convert to hex for readability

After that, you'll get p, q and d.

Then construct a private key PEM and voila! solved~